Weighted Automata

Why weights? Imagine a complicated machine, modeled by an automaton (deterministic or not). Imagine that each operation requires a quantity of energy (or time or some other resource) to be performed.

In the end you want to know the minimum amount of the resource needed for the machine operation.

Alternatively each transition can produce an amount of energy (or something else) and you are interested in the maximum amount produced.

Another scenario: imagine an automaton where transitions have a probability of execution¹ now you are interested in the total probability of a sequence of transitions.

Or again consider an ordinary automaton that accepts a regular language but now you want to know not only whether a word is accepted or not but also some characteristic of the accepted word (like the count of some letters).

All these scenarios can be modeled by adding weights to the definition of automata.

This post is an elementary introduction to weighted automata based mainly on  [1] and  [2]. The mathematics of weighted automata is very sophisticated/tricky I will skip most of it because in the end I am interested in automata learning (which I will cover in the next post).

For a very simple introduction to automata you can look here.

---

A weighted finite automaton (WFA) is made of (see  [3])

• a finite alphabet \(\Sigma = \{a,b,\dots,z\}\)
• a finite set of states \(Q = \{q_0,q_1,\dots,q_{N-1}\}\)

• a finite set of transitions \(T \subseteq Q \times \Sigma \times \mathbb{R} \times Q\) which are written as

  \[q \xrightarrow{\sigma:w} q'\]

• the initial weights \(\alpha_0,\alpha_1,\dots,\alpha_{N-1} \in \mathbb{R}\)
• the final weights \(\omega_0,\omega_1,\dots,\omega_{N-1} \in \mathbb{R}\)

and it processes a word \(a_0 a_1 \dots a_{k-1}\) like any non-weighted automata, that is it traces a path

\[p = p_0 \xrightarrow{a_0:w_0} p_1 \xrightarrow{a_1:w_1} p_2 \cdots \xrightarrow{a_{k-1}:w_{k-1}} p_k\]

but now each transition has a weight \(w_i\) and we take as the weight of the whole path their product (multiplied by the weights of the initial and final state)

\[w(p) = \alpha_{p_0} \left( \prod_{i=0}^{k-1} w_i \right) \omega_{p_k}\]

and since the definition allows for non-determinism we may have more than one path for the word \(a_0 a_1 \dots a_{k-1}\), how do we combine their weights?

We sum them

\[W(a_0 a_1 \dots a_{k-1}) = \sum_{p \in \text{ paths}(a_1 a_2 \dots a_{k-1})} w(p)\]

In short:

1. take a word
2. consider all the paths it traces in the WFA
3. for each path multiply the weights
4. multiply with the initial/final state weights
5. finally sum all the individual path weights

In the end a WFA computes a function

\[W: \Sigma^\star \to \mathbb{R}\]

Also we can say that a word is accepted if its weight is non-zero.

---

Here we have taken the weights to be real numbers, the definition you find in the literature usually is more general: it takes weights in a semiring.

The fact is that we only need to take products and sums of weights and a semiring is an algebraic structure that provides just that and nothing more, for example in a semiring numbers do not need to have an inverse.

I avoid semiring here because the learning algorithm that I will cover in the next post works only with real weights.

---

There is an easier way to compute \(W\), first lets redefine the \(N\) states WFA in this way

• let \(\boldsymbol{\alpha} = (\alpha_0,\alpha_1\dots,\alpha_{N-1})\) be the initial weight vector

• let \(\mathbf{A}^{(\sigma)}_{q,q'}\) be the \(N \times N\) weight matrix, its coefficients are the weights of the transitions

  \[q \xrightarrow{\sigma} q'\]

• let \(\boldsymbol{\omega} = (\omega_0,\omega_1\dots,\omega_{N-1})\) be the final weight vector

now the weight of a word \(a_0 a_1 \dots a_{k-1}\) is just the product

\[W(a_0 a_1 \dots a_{k-1}) = \boldsymbol{\alpha}^\top \mathbf{A}^{(a_0)} \mathbf{A}^{(a_1)} \cdots \mathbf{A}^{(a_{k-1})} \boldsymbol{\omega}\]

---

For example consider this two states WFA²

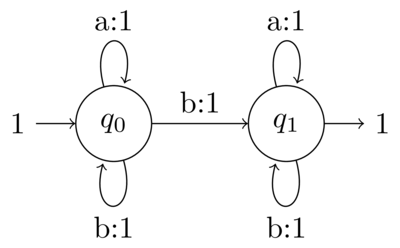
here \(q_0\) is the only starting state, \(q_1\) is the sole accepting state and note that \(q_0\) has two outgoing transitions for the letter "b" thus

\[\boldsymbol{\alpha} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \hspace{1cm} \mathbf{A}^{(a)} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \hspace{1cm} \mathbf{A}^{(b)} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \hspace{1cm} \boldsymbol{\omega} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\]

If you take any word \(w\) and make the matrix products in \(W(w)\) you immediately see that the "a"s do not contribute to the final weight (since \(\mathbf{A}^{(a)}\) is the identity). This leaves only the multiplication of as many \(\mathbf{A}^{(b)}\) as there are occurrences of "b" (\(\text{#b}\)):

\begin{align*} W(w) &= \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}^{(\text{#b})} \begin{bmatrix} 0 \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & \text{#b} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} \text{#b} \\ 1 \end{bmatrix} \\ &= \text{#b} \end{align*}

that is the automaton computes the number of "b"s in the word w.

But why it is so? Consider the word "aaabaaa" and look at how it works out:

• the automaton starts in state \(q_0\)
• reading the first "a"s it stays in \(q_0\)
• when it reads the first "b" the path bifurcate: we have both \(q_0 \to q_0\) and \(q_0 \to q_1\) (with weight 1)
• reading the other "a"s the automaton stays in either state

in the end we have only two paths: \(q_0 \to q_0\) and \(q_0 \to q_1\) (both with weight 1) but only the second ends in an accepting state, summing them up we get

\[W(aaabaaa) = 1\]

What happens when there are more "b"s? Every time the automaton gets a new "b" a new path \(q_0 \to q_1\) is spawned and since they end in an accepting state they are summed up.

If you want to experiment with WFAs you can try pyAutoSpec which is a simple Python library to demonstrate WFA learning. The previous example can be found here: pyAutoSpec/Simple Weighted Automata.ipynb.

---

We have seen that an ordinary automaton recognizes a regular language. Now the question is:

What is it that a WFA recognizes?

A language is just a subset of all the possible combinations of letters of an alphabet

\[\mathcal{L} = \{a, ab, aba, aabb, abbbaa, \dots\}\]

with a little imaginative effort we could add weights in front of the words

\[\mathcal{L} = \{ 0 \cdot a, 1 \cdot ab, 1 \cdot aba, 2 \cdot aabb, 3 \cdot abbbaa, \dots \}\]

it turns out that this trick can be made rigorous: let's define formal power series as a formal sum

\[\mathcal{S} = \sum_{w \in \Sigma^\star} \langle \mathcal{S}, w \rangle w\]

with coefficients \(\langle \mathcal{S}, w \rangle \in \mathbb{R}\), here formal means that we don't care if the sum converges or not, in the words of H.S. Wilf  [4]

Finally we can answer the question: the WFA \(A\) recognizes the formal power serie \(\mathcal{S}\) with coefficients

\[\langle \mathcal{S}, w \rangle = A(w)\]

and like we said that a language is regular when it is recognized by an automaton, we say that a power serie is rational when it is recognized by a WFA.

For the full account of the theory of rational power series see  [2] Chap.III Sec.2.

---

---