An Introduction to Automata

Why are automata so interesting? Automata are so simple that they fit in many places and situations.

You can use automata

to describe real machines (vending machines, industrial automations, etc.)
to validate protocols¹
as a language to express constraints²
as a basic machine learning model without much generalization power
to get insights on entangled quantum states³
for all kind of string search/manipulation algorithm

A deterministic finite automaton (DFA) is made of

a finite alphabet $Σ = {a, b, \dots, z}$ ⁴
a finite set of states $Q = {q_{0}, q_{1}, \dots, q_{N - 1}}$
a transition function $τ : Q \times Σ \to Q$
a starting state $q_{0} \in Q$
a set of accepting states $F \subseteq Q$

and it works in this way: you are given a word $w = a_{0} a_{1} \dots a_{n - 1}$

the automaton is initialized at state $q_{0}$
for each letter $a_{i}$ , starting from $i = 0$ , update the state to $q_{i + 1} = τ (q_{i}, a_{i})$
if the last state $q_{n}$ is an accepting state ( $q_{n} \in F$ ) then the word $w$ is accepted otherwise it is rejected

in the end the automaton computes a function

$f : Σ^{⋆} \to {accept, reject}$

The automaton is called deterministic because at each step it is in a definite state.

The state summarizes the relevant features (relevant for the final decision to accept or reject the word) of the input processed so far.

The language of an automaton is just the set of recognized words, the language recognized by a DFA is called regular.

The alphabet is different from application to application, for example:

for modeling machine the letters are events like the pushing of a button, the activation of a sensor etc.
for protocols they are actions performed by some party
for string algorithms they are just characters

For example consider the following DFA

and consider the word "byyxy"

it is accepted because the automaton ends up in state $q_{4}$ which is accepting.

The traversed states encode the relevant features of the word, for example state $q_{2}$ says that a "b" and zero or more of "y" have been seen. State $q_{1}$ means that for the purpose of further processing an "a" and a "byyx" (with any number of "y") are the same thing.

On the other hand the word "abx"

is rejected because the automaton is stuck in the non-accepting state $q_{3}$ .

So the automaton accepts a word if there is a path connecting the start state to the accepting state.

The same automaton can generate random words from its language by performing a random walk on its graph.

Another way to look at $τ$ is as a set of adjacency matrices, one for every letter $σ \in Σ$ , defined in this way

M_{i j}^{(σ)} = {\begin{cases} 1, & if τ (i, σ) = j \\ 0, & otherwise \end{cases}

Suppose you are given a word $w = a_{0} a_{1} \dots a_{n - 1}$ , to check if it is accepted or not you multiply the matrices corresponding to the letters

$M^{(w)} = M^{(a_{0})} \cdot M^{(a_{1})} \dots M^{(a_{n - 1})}$

the elements $M_{i j}^{(w)}$ count the number of paths $# (q_{i} \to q_{j})$ ⁵ so if $# (q_{0} \to q_{i}) = 1$ for some $q_{i} \in F$ then the word is accepted, otherwise it is rejected.

This can be seen easily for a length 2 path:

${[M^{(a)} \cdot M^{(b)}]}_{i j} = \sum_{k = 0}^{N - 1} δ_{τ (i, a), k} δ_{τ (k, b), j}$

the term inside the sum is non-zero only if there is a path $q_{i} \overset{a}{\to} q_{k} \overset{b}{\to} q_{j}$ (and since the automaton is deterministic there can be only one).

Take the word "byyxy" as an example, we can take

$M^{(b y y x y)} = M^{(b)} \cdot M^{(y)} \cdot M^{(y)} \cdot M^{(x)} \cdot M^{(y)}$

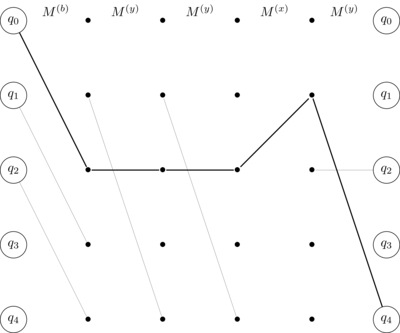
which is zero except for the entry $q_{0} \to q_{4}$ thus the word is accepted.

Can we make a DFA more powerful?

Imagine a machine that can be in more than one state at a time, this amounts to changing the DFA definition of $τ$ in this way

$τ : Q \times Σ \to P (Q)$

$τ$ now returns a set of states for each transition, the result is called a non-deterministic finite automaton (NFA)⁶.

Consider for example this NFA⁷

note that now, starting from $q_{0}$ , the letter "a" leads to two states $q_{0}$ and $q_{1}$ also "b" leads to $q_{0}$ and $q_{2}$ .

Consider the word "abab", the NFA performs these transitions

${q_{0}} \overset{a}{\to} {q_{0}, q_{1}} \overset{b}{\to} {q_{0}, q_{2}, q_{3}} \overset{a}{\to} {q_{0}, q_{1}, q_{3}} \overset{b}{\to} {q_{0}, q_{2}, q_{3}}$

which end in an accepting state.

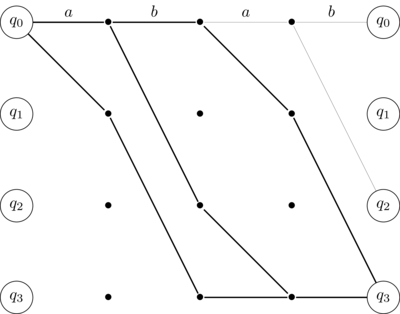
Note how the fact that the automaton can be in more than one state at once introduces multiple paths.

Now the question is:

Does this kind of flexibility lead to a richer structure of the accepted language? Does an NFA accept a larger language than a DFA?

Surprisingly the answer is NO?

Given an NFA it is always possible to build an equivalent DFA that accepts the same language through the subset construction.

The idea is to take $P (Q)$ as the set of states of the DFA (the powerset of the set of NFA's states) and to note that only a few of them will be needed.

Taking the previous example we can enumerate all the distinct states needed by the NFA

NFA	DFA
${q_{0}}$	$r_{0}$
${q_{0}, q_{1}}$	$r_{1}$
${q_{0}, q_{2}}$	$r_{2}$
${q_{0}, q_{1}, q_{3}}$	$r_{3}$
${q_{0}, q_{2}, q_{3}}$	$r_{4}$

adding the transitions the resulting DFA is

[1]

J. D. U. John E. Hopcroft Rajeev Motwani, Automata Theory, Languages, and Computation (Addison Wesley, 2006).

Footnotes:

see for example [1] Chap.2

for an example in operation research see GitHub - lucamarx/pywfplan: A Python library to plan a call center workforce

I hope to write more about this when I will understand it better

⁴

we denote the set of words made by letters in $Σ$ by $Σ^{⋆}$ which includes also the empty word $ϵ$

⁵

since the automaton is deterministic it can be only 0 or 1

⁶

a set of states is accepted if it contains at least one accepting state

⁷

it accepts any word that contains an "ab" or a "ba"